Kevin Brown, Brookhaven National Laboratory and Stony Brook University, and Sandra Biedron, Element Aero, the Center for Bright Beams, and the University of New Mexico
In 1959, Richard Feynman gave an inspiring and visionary seminar. The lecture he titled “There’s Plenty of Room at the Bottom” [1] was meant to focus on areas young physicists could pursue for their studies. The lecture walked the listeners down to smaller and smaller scales where Feynman’s powerful imagination took them from small-scale computers to writing an entire encyclopedia on the head of a pin to computing using small sets of atoms. While he did not really propose quantum computing as we know it today, his insights formed the foundation and motivation that has led to today’s technologies. To quote Feynman:
“When we get to the very, very small world – say circuits of seven atoms – we have a lot of new things that would happen that represent completely new opportunities for design. Atoms on a small scale behave like nothing on a large scale, for they satisfy the laws of quantum mechanics. So, as we go down and fiddle around with the atoms down there, we are working with different laws, and we can expect to do different things. We can manufacture in different ways. We can use, not just circuits, but some system involving the quantized energy levels, or the interactions of quantized spins, etc.”
To consider he said this in 1959 is amazing! Many technologies had to be invented before such a vision could be realized. These included the ion trap [2], methods for measuring and manipulating individual quantum systems[3], and experiments proving the violation of Bell inequalities [4] (which demonstrated quantum states can be entangled, a key ingredient to quantum computing.)
In 1934, Eugene Wigner predicted there should be a solid phase of electrons. Wigner crystals, a type of Coulomb crystal, have since been observed [5-10]. However, the development of laser cooling led to the observation of Coulomb crystals composed of ions. Groups led by David Wineland at NIST in Boulder, Colorado [11], and Herbert Walther at the Max-Planck Institute for Quantum Optics, Garching, Germany [12] used laser cooling techniques in ion traps to create some of the first ion Coulomb crystals. Over the past 35 years many groups have created and studied ion Coulomb crystals. In 1995, Juan (Ignacio) Cirac and Peter Zoller proposed the use of a linear ion trap as a platform for quantum computing [13]. Aware of the work by Wineland and Walther, they worked out the key ingredient for how to use multiple quantum states and entanglement to create quantum gates with trapped ions [14].
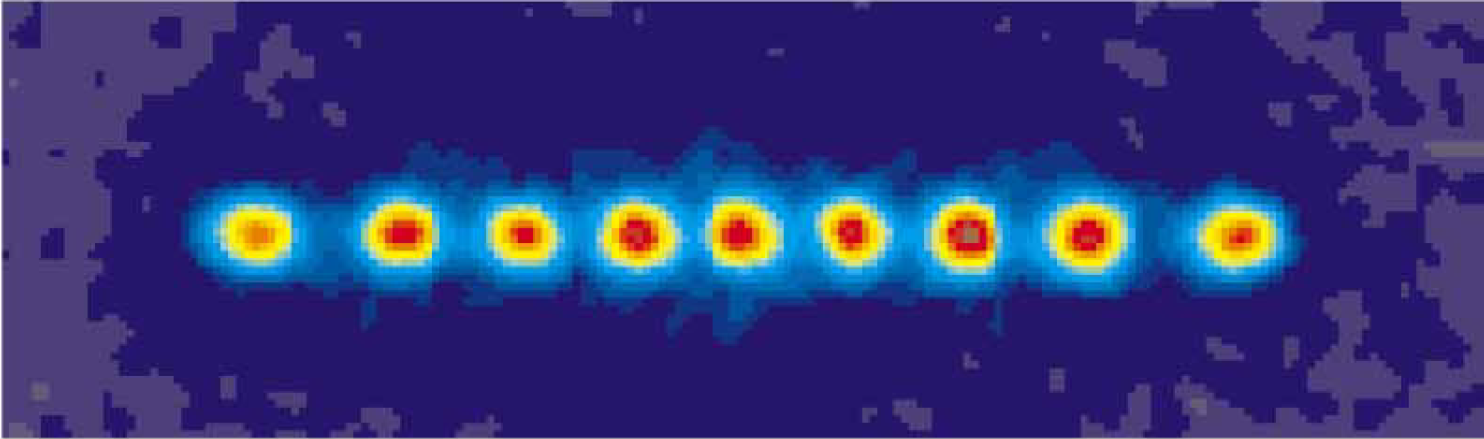 Figure 1: Picture of a nine-ion Coulomb crystal (Figure reprinted from Nägerl, H.C. et. al (1998) Applied Physics B. 66. 603-608., copyright 2014 Springer Nature.)
Figure 1: Picture of a nine-ion Coulomb crystal (Figure reprinted from Nägerl, H.C. et. al (1998) Applied Physics B. 66. 603-608., copyright 2014 Springer Nature.)
Coulomb Crystals
A crystalline beam is a collection of charged particles (either Wigner crystals with electrons or the ion crystals observed by Wineland’s and Walther’s groups) that have been cooled down to a level where the vibrational motion of the particles is too weak to overcome the Coulomb potential of adjacent particles (Figure 1). The particles form an ordered lattice. However, for these particles to be useful for quantum computing, they need to be cooled further, to the point where the quantized motional modes of the lattice are observable. Ions need to be cooled below the Doppler cooling limit by employing other cooling methods, such as Raman transition cooling or sympathetic cooling. Cooling to this level also minimizes the micromotion of the ions that is induced by the confining transverse rf potential of the ion trap [15].
Quantum computing using ion trap systems exploits two quantum properties, the external energy eigenstates, such as the axial center-of-mass motion of the string of ions in the trap, and the internal eigenstates of each ion in the string, such as the spin states of one of the orbital electrons in each ion. However, the quantized vibrational energy per mode n, is $E_n = 〈{n}| H_0 |{n}〉 = (n + \frac{1}{2}) \hbar \omega_0$, where $\omega_0$ is the fundamental frequency for the chain of ions and is a function of the Coulomb and other potentials holding the ions in the chain. As the number of ions increase, the number of modes also increase. An ensemble of ions of size N+1 has 3N+3 motional degrees of freedom, so as N becomes large, cooling and controlling the chain becomes very difficult.
Creating a qubit in ion traps involves excitation and measurement of stable or metastable internal states of individual ions, such as the hyperfine states. The basic method [16] is to excite specific hyperfine spin states where the two quantum states are either spin up or down ($|{\downarrow}〉$ or $|{\uparrow}〉$), corresponding to qubit logical $|{0}〉$ and $|{1}〉$ states. Using a polarized laser to scatter photons, the two distinct states can be observed. Light will scatter for only one of the states, allowing the states to be efficiently measured. Today’s systems use different ions and different lasers, but the basic technique remains the same.
Ion crystals have been created in many types of traps and accelerator systems. And they have many possible uses beyond quantum computing [17]. The main problem with ion traps is scaling to larger numbers of qubits. Researchers have devised many approaches, with small ions traps on chips, multiple ion traps in arrays and even circular ion traps in chips. These types of systems create stationary chains of ions and allow laser interactions in the laboratory frame. Ion crystals for quantum computing could be created and accelerated in a storage ring [18]. Such a configuration would allow scaling to large numbers of qubits without having to scale to a large number of lasers or large number of traps. The laser interactions, whether with a stationary or moving ion, are unchanged. In the case of a moving ion, the time to perform a state transition is restricted to the laser width divided by the ion’s velocity, unless the laser field can be moved and follow in the same reference frame. One approach around this may be to spread the laser field out along the path of the ion or to split the laser pulse repeatedly to spread the laser field along the path of the ion’s trajectory. More research is needed to develop these techniques [19].
Quantum Computing
As Feynman said, “If you want to make a simulation of nature, you’d better make it quantum mechanical” [20]. There is no rule that says because we call it a computer it has to look or even feel like a modern classical computer. But it does have to be a true quantum mechanical system. This is an important yet subtle point. If you could design an electrical circuit, for example, that could simulate quantum mechanical behavior, it would still not be a quantum mechanical system. This might be okay, as it might be able to very closely simulate some specific quantum mechanical phenomena. But such a system would not be a universal computer that can simulate any physics phenomena. On the other hand, if you could build a true quantum computer (equating true to mean the basis of the computational states is quantum mechanical in nature and not a simulation), that can simulate local quantum systems, such a computer could solve any classical problem as well [21].
This may not seem important, on the surface, since you might say, so what, a classical computer can do it. However, when you get into the theory of computing, there are very hard problems that can, in principle, be solved on a classical computer, but it might take an exceedingly long time. A quantum computer could solve such a problem in a much shorter amount of time. Problems that are both impossible or hard to solve on a classical computer can be solved on a quantum computer, sometimes much more easily and quickly (a more succinct description is shown in figure 2.)
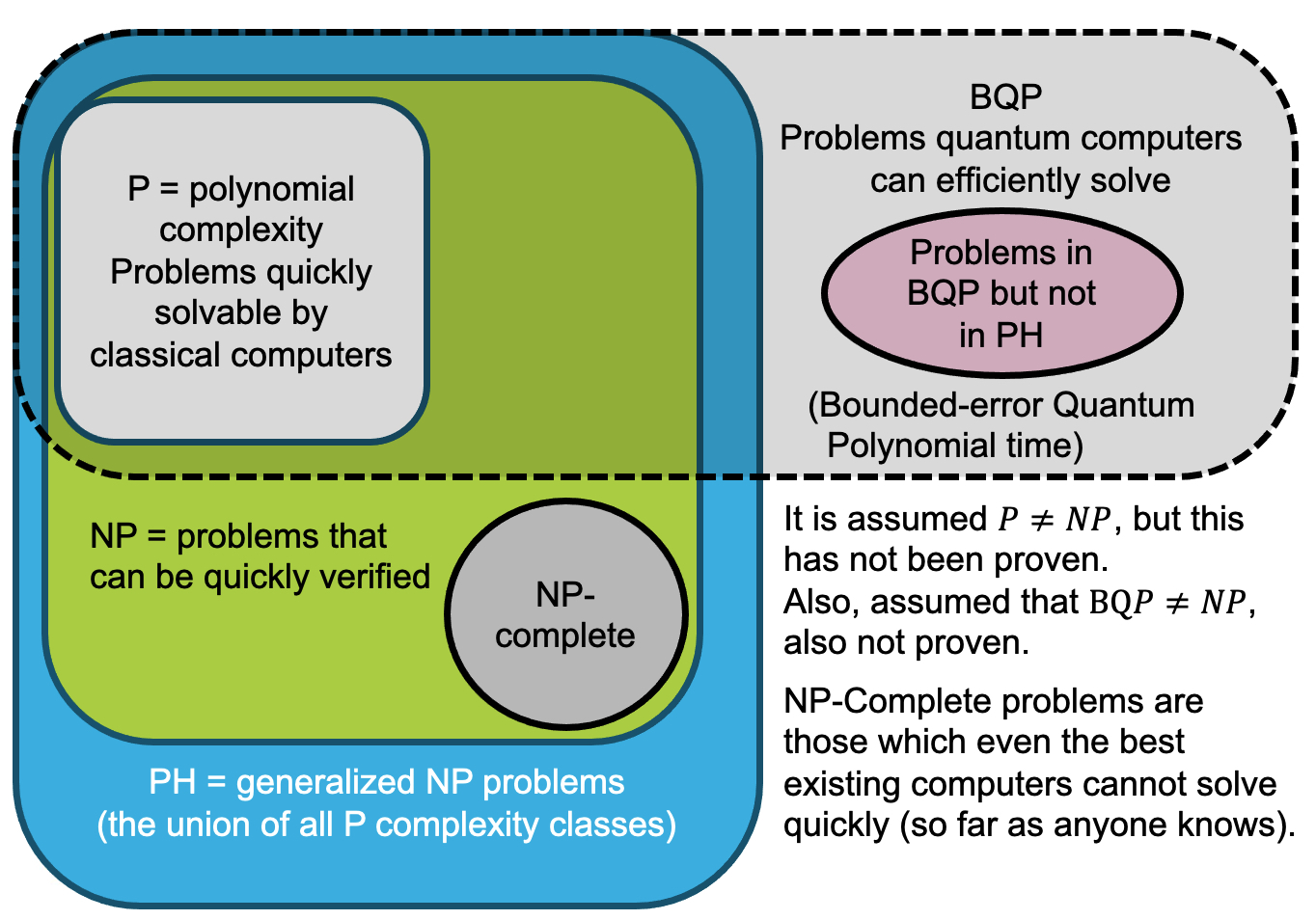 Figure 2: Euler diagram illustrating the relationships of different complexity classes for classical and quantum computing. This is an active area of research, so this diagram is only meant to generally show how different classes of problems fit into either a classical or quantum computing universe. Here P = polynomial complexity, NP = complexity problems easy to verify, NP - Complete = nondeterministic polynomial-time complete, PH = polynomial hard, and BQP = bounded-error quantum polynomial time. For a nice summary of the topic, see Scott Aaronson’s 2008 Scientific American article [22].
Figure 2: Euler diagram illustrating the relationships of different complexity classes for classical and quantum computing. This is an active area of research, so this diagram is only meant to generally show how different classes of problems fit into either a classical or quantum computing universe. Here P = polynomial complexity, NP = complexity problems easy to verify, NP - Complete = nondeterministic polynomial-time complete, PH = polynomial hard, and BQP = bounded-error quantum polynomial time. For a nice summary of the topic, see Scott Aaronson’s 2008 Scientific American article [22].
A qubit is a two-state system, such as the spin states described above. A key feature of quantum mechanics is such two-state systems hold each state in superposition. This is very different from a classical bit which is either a high or low voltage in some set of transistors. The qubit holds both the 0 and the 1, meaning there is a probability that either state will be observed when we measure the state. Such a quantum system, with two mutually orthogonal states, has a Hilbert space of two dimensions. If we have n qubits (e.g., n atoms in a Coulomb crystal) we have 2n mutually orthogonal quantum states. All these states are held in superposition in our crystal. In a classical computer, a register of n bits will hold a single number, when decoded from binary to base-10. In a quantum computer n qubits hold 2n numbers. Until we measure those states any of those numbers has a probability of arising as the result of that measurement.
We’ve learned how to make qubits using ions in a trap, but that is not enough to make a computer. We need to be able to make operations on those qubits, to run simulations. Those operations need logic gates. These are simple unitary operations, where through processes performed in time a qubits state evolves. In the simplest example we may have a state that evolves as $|{0}〉 \rightarrow |{0}〉$ or $|{0}〉 \rightarrow |{1}〉$. To do this requires something more than just the qubits. Imagine we could perform the following operation: $|{0}〉〈{0}| I + |{1}〉〈{1}| U$, where I is the single bit identity operation and U is some other single bit operation. The single bit operation is usually called a controlled U gate, since the action I or U on the second qubit is controlled by whether the first qubit is in the state $|{0}〉$ or $|{1}〉$. A classic example of such an operation would be a CNOT gate (or the quantum version). More logical operations require further qubits. A quantum AND operation requires a three-qubit controlled-controlled-NOT gate (also known as a Toffoli gate).
However, we have not really defined what a universal quantum computer is, beyond Feynman’s one requirement. What does it mean, from a practical level? Traditionally this would be defined by the DiVincenzo’s criteria, which state that a system is scalable, have means for initializing qubits, allow operations within decoherence times, have methods for a universal set of operations, and allow qubits to be easily read [23]. Ion traps with ultra-cold Coulomb crystals satisfy all these criteria, although there are devils in the details. Scaling to large numbers of qubits brings new challenges, such as keeping track of the qubits (uniquely identifying them) [24], working within the time constraints given by the coherence lifetime of the quantum states, and having means to handle errors.
Quantum mechanics brings new concepts into the arena, which are not a concern in classical computing. One of the most stringent is the no-cloning theorem. In a classical computer it is easy to make copies of the bit patterns in the memory registers. We rely on this ability to perform computations. However, in the quantum realm, we have to work differently. It is not possible to make a copy of an arbitrary unknown quantum state. Since we can’t know the state of some quantum system without measuring it, and since the act of measuring the state destroys it, we can’t make a copy. This goes back to the idea that a non-disturbing measurement scheme cannot exist [25-27].
Still Plenty of Room at the Bottom!
We have only touched the surface of this topic, and it is an extremely active area of research. There remain many questions to sort out and technologies need to be developed to bring Feynman’s original vision to reality. And there is much work going on in related areas: development of quantum algorithms and how to deploy them on a given platform, methods to correct errors and gain trust in the results, moving qubits over a network, and other ways to meet DiVincenzo’s criteria. In addition, what it means to compute a quantum algorithm is even an area of study. For example, to design new drugs, explore materials at the molecular level and to reproduce the behavior of such systems may mean combining the qubits to mimic these systems. Now, we would like to add to the challenges and suggest that there remain plenty of ideas to explore and other approaches to try. We discussed one-dimensional Coulomb crystals, but what about two- or three-dimensional crystals? Will this allow development of more complex protein molecules? What about crystals composed of multiple ion species? How can we control chains of ions to shuffle and move them as needed to solve a given simulation? Leveraging the talent and deep knowledge of the particle accelerator and beam dynamics community could greatly accelerate the development of true universal computers. These are the kinds of problems we are trained and have a passion to solve.
Acknowledgements
We wish to thank Professor Thomas Robertazzi, Stony Brook University, for reviewing the manuscript. This work is supported by Brookhaven Science Associates, LLC under Contract No. DE-SC0012704 with the U.S. Department of Energy.
[1] There’s Plenty of Room at the Bottom, Richard Feynman, https://calteches.library.caltech.edu/1976/1/1960Bottom.pdf
[2] The Nobel Prize in Physics 1989. NobelPrize.org. Nobel Prize Outreach AB 2024. Tue. 13 Aug 2024. https://www.nobelprize.org/prizes/physics/1989/summary
[3] The Nobel Prize in Physics 2012. NobelPrize.org. Nobel Prize Outreach AB 2024. Tue. 13 Aug 2024. https://www.nobelprize.org/prizes/physics/2012/summary
[4] The Nobel Prize in Physics 2022. NobelPrize.org. Nobel Prize Outreach AB 2024. Tue. 13 Aug 2024. https://www.nobelprize.org/prizes/physics/2022/summary
[5] C. Yannouleas, U. Landman, (2007). "Symmetry breaking and quantum correlations in finite systems: studies of quantum dots and ultracold Bose gases and related nuclear and chemical methods," Reports on Progress in Physics. 70 (12): 2067–2148. arXiv:0711.0637, doi:10.1088/0034-4885/70/12/R02
[6] E. Y. Andrei, G. Deville, D. C. Glattli, F. I. B. Williams, E. Paris, B. Etienne, (1988). "Observation of a magnetically induced Wigner solid," Physical Review Letters. 60 (26): 2765–2768. doi:10.1103/PhysRevLett.60.2765
[7] H. Zhu, Y.P. Chen, P. Jiang, L.W. Engel, D.C. Tsui, L.N. Pfeiffer, K.W. West, (2010). "Observation of a pinning mode in a Wigner solid with fractional quantum Hall excitations," Physical Review Letters. 105 (12): 126803. arXiv:1006.2335, doi:10.1103/PhysRevLett.105.126803
[8] J. Bylander, T. Duty, P. Delsing, (2005). "Current measurement by real-time counting of single electrons," Nature. 434 (7031): 361–364. arXiv:cond-mat/0411420, doi:10.1038/nature03375
[9] W.K. Hew, K.J. Thomas, M., Pepper, I. Farrer, D. Anderson, G.A.C. Jones, D.A. Ritchie, (2009). "Incipient Formation of an Electron Lattice in a Weakly Confined Quantum Wire," Physical Review Letters. 102 (5): 056804. arXiv:0907.1634, doi:10.1103/PhysRevLett.102.056804
[10] J. S. Meyer, K. A. Matveev, (January 2009). "Wigner Crystal Physics in Quantum Wires," J. Phys.: Condens. Matter. 21 (2): 023203. arXiv:0808.2076, doi:10.1088/0953-8984/21/2/023203
[11] D.J. Wineland, J.C. Bergquist, W.M. Itano, J.J. Bollinger, C.H. Manney, “Atomic-ion Coulomb clusters in an ion trap,” Phys. Rev. Lett. 59 (1987) 2935–2938. http://dx.doi.org/10.1103/PhysRevLett.59.2935.
[12] F. Diedrich, E. Peik, J.M. Chen, W. Quint, H. Walther, “Observation of a phase transition of stored laser-cooled ions,” Phys. Rev. Lett. 59 (1987) 2931–2934. http://dx.doi.org/10.1103/PhysRevLett.59.2931.
[13] J. I. Cirac and P. Zoller, 1995, “Quantum computations with cold trapped ions,” Phys. Rev. Lett. 74 4091–4
[14] J. I. Cirac, P. Zoller, H. J. Kimble and H., Mabuchi, 1997, “Quantum state transfer and entanglement distribution among distant nodes of a quantum network,” Phys. Rev. Lett. 78 3221
[15] D. Habs, and R. Grimm, "Crystalline Ion Beams, "Annual Review of Nuclear and Particle Science,” Volume 45, Review Article Vol. 45:391-428 (Volume publication date December 1995) https://doi.org/10.1146/annurev.ns.45.120195.002135
[16] D.J. Wineland, et al.,“Experimental primer on the trapped ion quantum computer,” Fortschr. Phys. 46 4-5, 363-390, 1998
[17] M. Drewsen, "Ion Coulomb Crystals,"Physica B: Condensed Matter, vol. 460, pp. 105-113, 2015, Special Issue on Electronic Crystals (ECRYS-2014) https://doi.org/10.1016/j.physb.2014.11.050
[18] K.A Brown and T. Roser, “Towards storage rings as quantum computers,” Phys. Rev. Accel. Beams, 23:054701, 2020, Erratum, Phys. Rev. Accel. Beams, 24:049901, 2021, doi:10.1103/PhysRevAccelBeams.23.054701
[19] T. Shaftan, T. and B.B. Blinov, “Cold ion beam in a storage ring as a platform for large-scale quantum computers and simulators: challenges and directions for research and development,” Phys. Rev. Accel. Beams 24, 094701, 2021, doi:10.1103/PhysRevAccelBeams.24.094701
[20] R.P. Feynman, “Simulating physics with computers,” International Journal of Theoretical Physics. 21 (6): 467–488, 1982
[21] S. Lloyd, “Universal quantum simulators,” Science, 273, 1073–1078, 1996, doi:10.1126/science.273.5278. 1073
[22] S. Aaronson, “The limits of quantum,” Scientific American, 2008
[23] D.P. DiVincenzo, “The physical implementation of quantum computation,” Fortschritte der Physik. 48 (9–11): 771–783. arXiv:quant-ph/0002077, 2000 doi:10.1002/1521-3978(200009)48:9/11<771:: AID-PROP771>3.0.CO;2-E
[24] B. Huang et al., "Artificial Intelligence-Assisted Design and Virtual Diagnostic for the Initial Condition of a Storage-Ring-Based Quantum Information System," IEEE Access, vol. 10, pp. 14350-14358, 2022, doi: 10.1109/ACCESS.2022.3147727.
[25] J. Park, (1970). "The concept of transition in quantum mechanics," Foundations of Physics. 1 (1): 23–33. doi:10.1007/BF00708652.
[26] W. Wootters and W. Zurek, (1982). "A Single Quantum Cannot be Cloned,” Nature. 299 (5886): 802–803. doi:10.1038/299802a0
[27] D. Dieks, (1982). "Communication by EPR devices," Physics Letters A. 92 (6): 271–272. doi:10.1016/0375-9601(82)90084-6