January 2023 Newsletter

Editor's Comments

I try to include in this newsletter items that are not only interesting and relevant, but also timely. The last requirement is usually a pleasure. In this issue, however, I deeply regret that the article by Prager and von Hippel on the nuclear threat associated with the war in the Ukraine is extremely timely. There is, in my opinion, a very serious threat of nuclear war starting there, the most serious threat of this kind I have seen in my lifetime. And I do not see a solution: if Putin loses, he might start a nuclear war in desperation. If he wins, he will be emboldened by his success and in due course start next another war against another neighbor: Estonia, Georgia, Kazakhstan... and it will be a progression towards WWIII similar to the one that lead to WWII in the thirties. And WWIII would be the end of the world. Also in this issue we have a very pedagogical article by Reed on how Uranium isotope separation actually works, and what parts are easy and which are difficult. And a third article on the Rare Earths scarcity problem.

As always, I remind you that the contents of this newsletter are largely reader driven. Please send your contributions 8 Rare Earth Supply Chain Challenges: Action Items for the Physics Community, Julie Michelle Klinger R E V I E W S 10 Dignity in a Digital Age: Making Tech Work for All of Us, by Ro Khanna Reviewed by Quinn Campagna and your suggestions. All topics related to Physics and Society, very broadly understood, are welcome. No pertinent controversial subject needs to be avoided. Content is not peer reviewed and opinions given are the author’s only, not necessarily mine, nor the Forum’s nor, a fortiori, the APS’s either. Letters to the Editor for publication are also welcome.

The APS production people prefer MSWord formats. Everything goes to me except Book Reviews which should be sent directly to the new book reviews editor Quinn Campagna.

Oriol T. Valls                                                                                                                                          
University of Minnesota                                                                                                                             

Top

Articles

Nuclear War Dangers from the Ukraine Conflict: And a Cautionary Statement for Scientists to Sign

Stewart Prager and Frank von Hippel, Princeton University

President Putin's threats to use nuclear weapons in the Ukraine war are alarming. His recent statements include:

“Whoever tries to interfere with us should know that Russia’s response will be immediate and will lead you to such consequences as you have never experienced in your history.” “This is not a bluff.” Russia “is today one of the most powerful nuclear states.”

President Biden has commented that the situation is as close to “Armageddon” as any time since the 1962 Cuban missile crisis. Putin has available to him sufficient nuclear weapons to annihilate rapidly any city or nation of his choice.

At least three lessons are confirmed by Putin's nuclear threats:

1. As long as nuclear weapons exist, national leaders under duress will resort to nuclear threats and, eventually, one of those threats will be carried out. Putin’s threats are not a “bug” of the nuclear world order, but an intrinsic feature.
2. We cannot predict when a leader of one of the nine nations that possess nuclear weapons will make nuclear threats or use nuclear weapons, or under what circumstances; but we can be confident that national leaders will do so many times in the future. The predictability is analogous to that of extreme climate events. Climate science foresees with confidence the increasing frequency of extreme weather events but it cannot predict where or when such events will occur.
3. Perhaps the most important lesson is the sheer insanity of a situation in which the psychology of one man holds the world hostage. Rational analysis plays little role relative to Putin’s fantasies about restoring Russia's empire. This is not unique to Putin or the current crisis. Many of us held our breath while President Trump and Kim Jong-un compared the sizes of their nuclear buttons. It is not clear if any of the leaders of the world's nine nuclear-armed states are subject to checks on their authority to launch nuclear weapons and kill millions to billions of human beings. There is no democracy when it comes to decisions to use nuclear weapons.

Some will argue that Putin is uniquely irresponsible in upsetting the stable nuclear world order and breaking the taboo against nuclear threats that has developed as a result of 77 years of nonuse since the US introduced nuclear weapons to the world by destroying Hiroshima and Nagasaki (which Putin cited as a "precedent").

The nuclear world order was never stable, however, and the taboo had been previously broken. The US leveled nuclear threats against North Korea and China during the Korean War before they acquired their own nuclear weapons, and against North Vietnam during the Vietnam War. The dangerous instability of the nuclear world has been evidenced by many close calls: the Cuban Missile Crisis of 1962, the Berlin Crisis of 1961, three US false warnings of attack in 1979 and 1980, and three Soviet/Russian false warnings in 1983 and 1995.

Given that Russia and the US have their vulnerable silobased intercontinental ballistic missiles (ICBMs) in launchon- warning postures, such false warnings are extremely dangerous. The early-warning crews have only minutes to determine if a warning is true or false, and the leaders have only minutes to determine whether or not to launch. The Pentagon expects China to adopt a similar launch-on-warning posture for the hundreds of ICBMs for which it is now building silos. The growth of China’s nuclear arsenal is turning a two-body problem into a more complex three-body problem. Add hackers to this mix and what could go wrong?

The problem with nuclear weapons lies not in the leaderships, but in the weapons themselves. We are not safe no matter who currently controls the weapons.

An unfortunate potential outcome of the current situation is that it could encourage further proliferation of nuclear weapons. When the Soviet Union disintegrated in 1991, Ukraine inherited about 1900 nuclear warheads on ICBMs and several thousand tactical nuclear weapons. Ukraine suddenly became the owner of the world's third largest nuclear weapon stockpile. In 1994, Ukraine agreed to transfer these nuclear weapons to Russia. In return, Russia (along with the US and the Great Britain) signed the Budapest Memorandum in which they pledged “to respect the independence and sovereignty and the existing borders of Ukraine.” Russia has violated this agreement. Some leaders of non-nuclear-weapon states ask: Would Russia have invaded had Ukraine retained some of its nuclear weapons? Would Saddam Hussein and Muammar Gaddafi be alive today if they had not given up their nuclear-weapon programs?

We do not know how the Ukraine situation would have unfolded if nuclear weapons did not exist. They have provided Putin a shield under which to invade Ukraine, knowing that his arsenal would deter the US and its NATO allies from fighting alongside Ukraine. Or perhaps, if he had invaded Ukraine anyway, NATO's entry into the fight, would have led to World War III. No one knows. What we do know is that the presence of nuclear weapons in the mix creates a civilizational risk that would not otherwise be present.

While these dangers are well beyond the scope of the physics community, there is much that we can do. Physicists have a special relation to nuclear weapons and, thereby, an opportunity to speak out on this issue with greater influence than others. We should seize this moment to warn against reckless threats of nuclear use.

To this end, we invite all physicists to sign a statement by scientists that condemns all threats of nuclear use. Other sectors of society have issued similar statements that will be bolstered by the scientists' statement. You can read the statement (and sign if you wish) here. The statement has been coordinated by the Physicists Coalition Nuclear Threat Reduction. We invite interested physicists to join the Physicists Coalition, an organization supported for its first two years by the APS and became independent this fall. Its mission is to provide its membership with information and opportunities for advocacy on nuclear weapons policy.

Top

Reviews

Dignity in a Digital Age: Making Tech Work for All of Us

Ro Khanna (Simon and Schuster, 2022), 354 pages, ISBN 978-1-9821-6334-1

In Dignity in a Digital Age, Silicon Valley Congressman Ro Khanna discusses the challenges and opportunities presented to the many areas of the United States that have been left behind by a rapidly changing tech-oriented economy. In the process, he lays out substantive policy proposals to begin addressing these problems. Additionally, Congressman Khanna argues that these developments must have an ethical and moral component behind them, and so dedicates much time to discussing how the structure of the digital world can be changed to improve its impact on society.

Part I of the book deals primarily with the economic aspects of the digital revolution.

Khanna points out that the digital revolution of the 21st century has disproportionally benefitted urban, white men, while leaving behind most other geographic, racial, and gender groups. In the process, communities have grown suspicious of tech developments, even when they can provide opportunities to overcome long-standing problems such as generational poverty and economic stagnation. Thus far, says Khanna, many of the proponents of such developments have been seen as carpetbaggers coming in to supplant the local community and culture of rural folks, and as a gentrifying force that pushes out marginalized groups. In order to combat this and maintain a healthy society, he argues, rural communities and communities of color must be included in the benefits of tech progress. Accomplishing this goal requires cooperation between the private and public sectors.

From the side of the government, Khanna proposes a wide range of policies that would decentralize and diversify the digital revolution, from the development of tech literacy programs at land grant colleges to the creation of tax incentives for investing in minority- and female-led businesses. For industry partners, he recommends that more recruitment and job training programs be tailored to the needs of local communities, rather than simply extracting value from them. With a combination of these efforts, Khanna asserts, the US can grow strong and lasting institutions that allow more people to benefit from the advances of the tech revolution.

Part II focuses on the civic and societal impacts of the tech industry. Khanna starts by making a very important point: that our lawmakers do not have the technological knowledge to properly legislate the digital world. In order for people and communities to enjoy the benefits of the tech economy, we must ensure that individuals are protected from abuses of power by tech companies. The congressman puts forward an Internet Bill of Rights, which would be meant to protect users from such events. It would include laws guaranteeing the right to actively opt-in to or out of data collection, to delete your personal data from digital platforms, and many others.

Of course, this is only part of the story. As has become evident in the past decade, technology can be used to bring about both great benefit and great harm to society. Khanna points to, on the one hand, the Arab Spring movement and, on the other, the January 6 insurrection. In order to fulfill the promises of the digital age, the US must promote the former and minimize the latter. This, of course, leads to the difficult problem of balancing freedom of speech with the prevention of hate speech, disinformation, and the incitement of violence.

While there are existing precedents in this vein for “analog” speech which apply, Khanna contends that the US must implement policies that promote counter speech against these things, enact stronger laws against actual acts of discrimination and violence, and raise the average level of digital literacy to truly be effective.

As is the nature of anything with the scope of this book, there is much to debate within Khanna’s arguments. He himself acknowledges this, giving examples of challenges faced when implementing similar policies. However, Dignity in a Digital Age sets forward a comprehensive series of goals and principles to guide the democratization of the digital revolution, and proposes a plan of action to implement it. As with all experiments, it may be found that there are better ways of accomplishing those goals, but in order to learn we must first make the attempt.

Quinn Campagna
University of Mississippi

Top

Rare Earth Supply Chain Challenges: Action Items for the Physics Community

Julie Michelle Klinger, PhD, Department of Geography and Spatial Sciences, University of Delaware, klinger@udel.edu

The advancement of physics relies on specialized technology that contains critical minerals and metals, such as rare earth elements (REEs). The fantastic magnetic, conductive, and optical properties of REEs, which includes elements 57-71 on the periodic table, as well as Scandium (21) and Yttrium (39), have been harnessed to build the equipment through which we expand our knowledge about the fundamental nature of the universe. For example, particle accelerators (https:// ui.adsabs.harvard.edu/abs/1978recp.work...27S/abstract) use magnets made with Samarium (62), Neodymium (60), and Praseodymium (59). Erbium(68)-doped filters on spectrographs (https://ui.adsabs.harvard.edu/abs/1978recp.work...27S/abstract) aboard the JWST and other telescopes are changing the way we see the cosmos. Dysprosium (66) is used in the quest to detect neutrinos (https://arxiv.org/abs/2106.06626). Lanthanum is used on lenses of consumer and advanced cameras. The list goes on.

This means that physics research depends on rare earth and other critical mineral supply chains (https://pubs.acs. org/doi/full/10.1021/acs.est.6b05751) that periodically feature in shocking news stories (https://www.globalwitness.org/ en/press-releases/new-evidence-shows-massive-and-rapidexpansion- illicit-rare-earths-industry-myanmar-fuellinghuman- rights-abuses-environmental-destruction-and-funding- military-linked-militias/) about social and environmental violence in mining sites around the world. It also means that experimental physics could be vulnerable to unpredictable supply chain disruptions due to conflict or poor planning. In an era of intensifying climate crises and increasing competition for critical raw materials, it is important for physicists, and those who support their research, to think about where the minerals and metals comprising their equipment come from; the conditions of their extraction, processing, and disposal; and more broadly, about the sectors in which critical minerals are used.

Rare earths are not rare, but the term persists long after their 1788 discovery in Ytterby, Sweden likely because of the imaginaries it fuels and the politics it enables. Put simply, if you call something rare, you think about it differently: all of a sudden, going to great lengths to acquire this or that member of the lanthanide series might seem not only reasonable, but unavoidable. For years, confusion about this fundamental fact led to the misperception that the social and environmental devastation that characterized China’s monopoly over rare earth mining was inevitable, which I write about in my book (https://www.cornellpress.cornell.edu/book/9781501714610/ rare-earth-frontiers/).

Although rare earths are not rare, there are serious concerns about whether there will be enough to build the infrastructure required to move away from fossil fuels, given the projected materials needs. This worry has only intensified in recent years, with the growth in demand for batteries and magnets, particularly for electric vehicles (https://www.sciencedirect. com/science/article/abs/pii/S2352550919304713), but also with the increased production of consumer electronics, space based and space-linked technologies, and the unchecked expansion of the military industrial complex, all of which require rare earth elements. These worries are fueling the drive to open new mines in sensitive ecosystems. But these days, rare earth elements are most often in the news under some variation of the misleading headline: Green Energy’s Dirty Little Secret.

This headline is misleading because EVs, and renewable energy, are only part of the story. Rare earth elements are important to every major form of energy generation: nuclear, hydro, renewable, and fossil. In fact, for decades, the primary reason REEs were imported into the US was for use in petroleum refining. Although the environmental, social, and economic issues plaguing supply chains are real, suggesting that these issues are unique to renewable energy technology does little more than stymie the long-overdue transition away from fossil fuels and protects other high-demand sectors from scrutiny. It is more accurate to say that rare earths are essential to the hardware of life as we know it, therefore no sector is exempt from the responsibility to rationalize supply chains or prevent their misallocation to destructive applications.

This is especially important when we talk about the materials needed to bridge the growing infrastructure gap (https:// pubs.acs.org/doi/10.1021/acs.est.2c05413). If we are on the eve of a massive critical materials shortage, and that shortage may undermine our chances of limiting global warming, what does that mean for physics research? As members of a scientific community with no problem understanding climate change, most physicists would likely accept, in principle and with some caveats, the slowdown of certain rare earth supply chains in order to build out renewable energy infrastructure with the scale and speed that is required. If shortage is on the horizon and demand comes from many sectors, then surely some prioritization is necessary to ensure that we don’t fall short of our climate goals, by guaranteeing, for example, that the industries that serve renewable energy infrastructure construction will receive the materials they need. No such policy exists, so it is possible that the rush to open new mines in the name of climate won’t ultimately provide materials for the renewable energy transition or help us address the climate emergency, not when fossil fuel and military applications command so much of the market share of critical materials—and produce so much of the global share (https://mitpress.mit. edu/9780262047487/the-pentagon-climate-change-and-war/) of greenhouse gas emissions.

This may seem like an intractable problem, but physicists have a history of taking on massively complex issues. Physicists can use their scientific authority and public standing to advocate for rational sourcing and allocation of rare earth elements and other critical materials in light of the climate emergency (https://today.oregonstate.edu/news/world-scientists- declare-climate-emergency-establish-global-indicatorseffective- action). There are three things to do.

To support the renewable energy transition, physicists can help campaign to establish sensible limits to the market share of rare earths and other energy-critical materials that can be captured by fossil fuel and major polluting interests. By any credible calculation, if we are serious about moving away from fossil fuel generation while maintaining steady economic growth (https://www.researchgate.net/profile/Simon-Michaux- 2/publication/351712079_The_Mining_of_Minerals_and_ the_Limits_to_Growth/links/60a62816a6fdcc3507dd1b4b/ The-Mining-of-Minerals-and-the-Limits-to-Growth.pdf), then there simply are not enough critical resources to go around. This means that we need sensible and anticipatory resource allocation policy. This is a high-stakes fight that bucks powerful trends and entrenched ideologies, which, like the work of the Union of Concerned Scientists, the Physicists Coalition for Nuclear Threat Reduction, and the Alliance of World Scientists, requires sustained grassroots outreach and education, high-level policy engagement, and high-profile advocacy. Like these other coalitions, this requires taking on powerful interest groups to redirect funding, power, and credibility away from activities that pose existential threats and toward activities that improve peace, security, and sustainability.

To help ease pressures to open new mines, institutions and lab managers can request—and eventually require—that discarded equipment be recycled by reputable firms. Physicists, the great institutions that support them, and the companies providing lab equipment (and insurance) all have a direct role to play in rescuing rare earths and other critical materials from waste streams by developing sensible repair and refurbishment procedures, and by ensuring that rare earths and other critical materials are recycled, reclaimed, and reused when, say, a cyclotron is dismantled, or lab equipment is updated.

To support innovation in the renewable energy transition and smarter materials use, funders and institutions can prioritize research that develops new methods (https://www. science.org/content/article/electric-jolt-salvages-valuablemetals- waste) to reclaim and recycle rare earths and other critical materials from waste to help build a circular economy. Over the past decade, I have interviewed scientists at public and private research institutions that had no other choice than to make their experiments with recycling and critical materials recovery a hobby or a side project, because they simply could not get funding to work on it full time. This has to change. Federal funding agencies and private foundations are a central part of setting the agenda to accelerate the growth of the circular economy, and there is an untapped pool of enthusiastic talent ready to take the lead on this crucial paradigm shift.

These are critical long-term efforts, but many folks simply might not have the bandwidth to take this on. That’s understandable. In the meantime, there are a few simple actions that can add up to big changes. Starting today, physicists can cultivate a deeper curiosity into the origins and life stories of the materials that comprise their equipment. They can share this curiosity, their questions, and their discoveries with their students and colleagues. Procurement offices and lab managers can ask their suppliers where the elements in certain components come from. Not just: where was this made, but where did the actual raw materials come from—the samarium in the magnets, the lanthanum in the lenses, the dysprosium in the lasers?

Most likely, most people will not know the answers to these basic questions. At least not at first. And chances are, those who do uncover answers will find them troubling. This is because the materials comprising scientific equipment provide a direct physical link to a host of social, environmental, and political problems from which the discipline has historically tried to distance itself (https://www.sciencenews.org/archive/ politics-and-physics). But learning—and teaching others—to see whole new webs of relations embedded in the material world around us is what the discipline does best.

Top

The Devil’s Work: A Maxwell's Demon Model for Understanding the Work Cost of Isotope Enrichment

B. Cameron Reed, Department of Physics (Emeritus), Alma College, camfissile@icloud.com

1. INTRODUCTION
Potential nuclear proliferation remains a concern for policymakers. Followers of proliferation affairs will know that uranium occurs in two isotopes, ²³⁵U and ²³⁸U, but that only the former can be used to make a bomb. Because these isotopes occur in nature in very unequal proportions (about 0.72% and 99.28%, respectively), it is necessary, if one desires to make a uranium-based fission bomb, to process a supply of ore to enrich the abundance of ²³⁵U to up to about 90%. What can seem very counter-intuitive, however, is to learn that much more work is required to raise the enrichment level from the natural level to, say, 20% than is required to go from 20% to 90%. While this has to be qualified with information about the masses involved, it is fundamentally true and is the reason that non-proliferation experts become concerned when a country’s enrichment capacity begins to exceed the 3-5% level typical of reactor fuel. Unfortunately, a rigorous derivation of the expression for the amount of work involved in enrichment is very complex. [1-3] The result of such analyses is an unusual second-order differential equation, the solution of which, Eqs. (8) and (9) below, is not at all obvious. The purpose of this article is to offer a mini-tutorial on enrichment and a simplified model of its energy cost based on imagining a Maxwell's demon-type creature who can sort isotopes by their weight. This treatment should be accessible to any reader familiar with basic concepts of probabilities, and the result gives numerical predictions which prove to be in remarkably good accord with the rigorous result.

Sections 2 and 3 of this paper cover some preliminaries. Uranium is normally a metal, and in the enrichment industry it must first be rendered into gaseous form for processing; the preferred current process is to employ cascades of centrifuges. To this end, the usual working material is uranium hexafluoride, UF₆, colloquially known as “hex”. Hex is a powder at room temperature and can be easily stored and transported, but it sublimes directly to a gas when heated to above about 60 C, making it ideal for use in centrifuges. The fluorine is later removed by chemical means to leave behind uranium metal or perhaps an oxide. Section 2 explores the arithmetic of determining exactly what mass of ²³⁵U is contained within a given mass of hex that has been enriched to a specified ²³⁵U abundance. This is strictly a separate issue from the energy cost of enrichment, but is included here for sake of completeness.

Any enrichment method will require energy to operate: gases must be pumped into and out of centrifuges, which must be spun. For enrichment engineers, the currency of the realm is known as the “Separative Work Unit.” Abbreviated SWU and pronounced “swoo,” these numbers quantify the energy cost of achieving the desired feed-to-product enrichment. SWUs are strictly a measure of energy, but the custom in the trade is to quote them in units of “kg-SWU,” a measure of the energy required to produce one kilogram of hex whose uranium content has been enriched to a specified percentage of ²³⁵U. Enrichment facilities are usually characterized by their annual kg-SWU capacities, although some large commercial firms cite their capacities in tonne-SWU per year, where tonne refers to the metric ton of 1,000 kg.

To compute a SWU value requires five elements of input data. These are the number of kilograms of feed material, the number of kilograms of product material, the enrichment level of the feed material, the desired enrichment level of the product material, and the enrichment level of the leftover waste or “tails” material, which will be less than that of the feed material. Section 3 sets up the key relationship between these parameters. The demon-inspired separation model is set up in section 4, its predictions are compared to those of the rigorous SWU expression, and some numerical examples are given. Section 5 offers some comments on current worldwide enrichment capacity.

2.  HEX AND ²³⁵U MASSES
Fluorine consists of only one isotope, ¹⁹F, that is, it has atomic weight 19 grams per mole. In this paper, I ignore the very slight non-integer values of the atomic weights of the elements and isotopes involved. Hex molecules containing ²³⁵U atoms will then have an atomic weight of 235 + 6(19) = 349 gr/mol, while those bearing ²³⁸U atoms will weigh in at 352 gr/mol. Now suppose that you have a sample of hex where the fraction of molecules containing ²³⁵U atoms is f₂₃₅. The overall atomic weight of the sample will be A_hex = 349 f₂₃₅ + 352(1– f₂₃₅), that is, (352 – 3 f₂₃₅) gr/mol. From basic chemistry, if the mass of the sample is M_hex grams, then the number of moles of hex must be M_hex/A_hex. The number of moles of ²³⁵U atoms in the sample will then be f₂₃₅ (M_hex / A_hex) and the mass of ²³⁵U will be this number times 235 gr/mol:
For a sample of hex that has been enriched to contain only atoms of ²³⁵U, the mass of ²³⁵U contained therein can never exceed (235/349) = 0.673 times the mass of the sample. To optimize compactness and efficiency, most commercial power reactors operate with fuel enriched to a concentration of typically 3.5% ²³⁵U: f₂₃₅ = 0.035. This is known in the nuclear trade as Low-Enriched Uranium, or LEU. By International Atomic Energy Agency definition, LEU extends up to 20% ²³⁵U; beyond this one has Highly-Enriched Uranium, or HEU. Many research and medical isotope-production reactors operate with fuel enriched to near the LEU/HEU transition value. Beyond a ²³⁵U content of 90% one has weapons-grade uranium. Some very compact reactors designed for use in naval vessels operate with very highly enriched uranium, but for countries whose nuclear activities are for the purposes of power production there is usually no need to enrich beyond a few percent.

3. FEED, PRODUCT, AND WASTE
In an enrichment process, a sample of hex known as the “Feed” is introduced into the operating machinery. Let the number of molecules or mass of feed material be F, and designate its ²³⁵U concentration as f_F as defined above. From this, the enrichment process is desired to yield mass P of product enriched to concentration f_P. Left behind will be W = F – P molecules or kilograms of waste material whose concentration f_W will be less than that of the feed material. The waste material is also known as “depleted” in that its content of ²³⁵U has been depleted relative to that of the feed material. In the enrichment community, the term “tails” is synonymous with waste; a typical tails concentration is 0.25%, or f_W = 0.0025. Figure 1 illustrates the idea of an enrichment process in schematic form.
For practical purposes, you will probably want to know what mass of product can be obtained from a given mass of hex feed and set of concentrations. An expression for this can be derived by demanding that both mass and number of moles of material be conserved: F = P + W and F/AF = P/AP + W/AW , where the A’s designate atomic weights. Eliminating W from these two expressions leads toThis can be simplified without any significant loss of accuracy. At most, f_P can approach unity, so even if f_F is very small, the first bracketed term on the right side can never drop below (349/352) = 0.9915. At the other extreme, this term can never exceed unity, so we are quite safe in dropping it and simplifying to In Eqs. (1) and (3), masses, P, and F are usually assumed to be in kilograms, but can equally well be in numbers of molecules or just a more generic “units”.

It may seem strange that we can specify all three of f_F, f_P, and f_W for a given amount of feed material within the obvious constraint that we must have f_P > f_F > f_W. The price paid for this liberty is that for fixed values of f_F and f_W, the amount of product obtainable from a given amount of feed drops steadily as f_P increases; this will be discussed in the context of Fig. 4 below.

Here is an example of using Eqs. (1) and (3) together. Suppose that a putative bomb-making country has 10,000 kg of hex already enriched to 5% ²³⁵U. If this is to be enriched in one step to a product of concentration of 90% along with tails of concentration 0.25%, then Eq. (3) indicates that we can expect to recover (10,000 kg)(0.05 – 0.0025)/(0.9 – 0.0025) = 529 kg of product if there are no losses in the machinery. Equation (1) then indicates that this product would have a ²³⁵U content of (529 kg)(235)(0.9)/[352 ¬– 3(0.9)] = 320 kg. This would be enough for about five Hiroshima-type Little Boy bombs.

4. ENTER THE DEMON
This section describes a simplified model for the work involved in enrichment.

To begin, imagine that the feed material of F molecules or kilograms and ²³⁵U concentration f_F is contained within a chamber. This is sketched in Figure 2. The demon begins by inserting a barrier (vertical line) into the chamber to divide it into waste (left, W) and product (right, P) sides, in such a way that the desired number of product molecules P as dictated by Eq. (3) find themselves in the right side, and hence the desired number of waste molecules W remain in the left side. Initially, the number of ²³⁵U molecules in the right side will be f_F P, whereas what is desired is f_F P molecules of this type. This means that (f_P - f_F)P molecules containing ²³⁵U atoms have to be shifted from the W side to the P side, while the same number of molecules containing ²³⁸U atoms will have to be shifted from P to W. The demon has work to do.

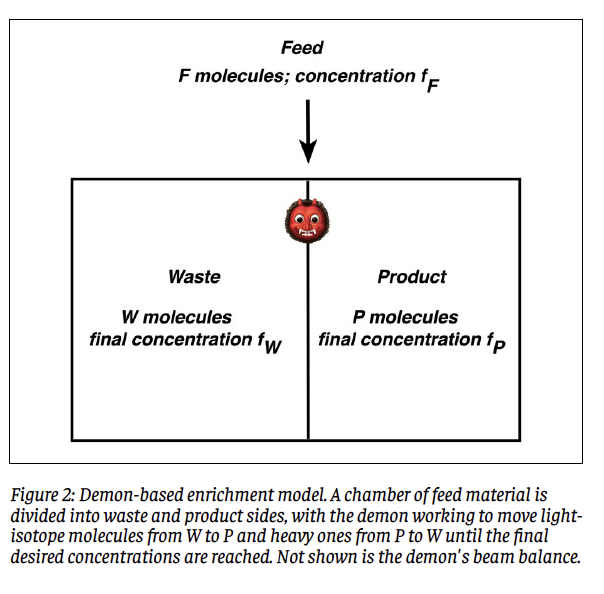
Now, the demon cannot tell lighter from heavier molecules merely by looking at them; he has to weigh them. To this end, we provide him with a beam balance. The fundamental idea is that the demon performs rounds of drawing pairs of molecules from each side and weighing them. Suppose that he starts with the W side. If he draws two light or two heavy molecules, the balance will not be able to discriminate between them and he will have to toss them back and make another draw. At some point he will draw one light and one heavy molecule, and he can set the light one aside for transfer to side P while returning the heavy one to W. He then repeats this procedure on the P side until he isolates a heavy molecule to be shunted to the W side. The two chosen molecules are dumped into their new homes, and the process begun anew for a second round of pair-drawings. Here is the key assumption: That the amount of work performed in any round of drawings is taken to be the inverse of the probability of drawing two dissimilar molecules. The rationale behind this assignment is that a low (high) probability will translate to a larger (smaller) number of pair-drawings, each one of which takes effort on the part of the demon. He continues in this way until the desired final conditions have been achieved, accumulating work along the way. An important point to be accounted for is that the isotopic concentrations will alter ever so slightly upon each round of draws. Since the proportion of sought-after molecules decreases on each side with each round, the work required will increase with each round but the number of remaining required rounds will steadily decrease. The total work required will reflect the competition between these effects. To be sure, one can imagine many hypothetical ways of performing such a separation procedure. A feature of this model is that the density of particles in each side of the chamber remains constant as drawings proceed.

To quantify this, imagine the sequence of draws from the W side of the container. In the first round, the probability of drawing dissimilar molecules will be 2 f_F (f_F – 1), with the factor of two arising from the possible draw sequences (light, heavy) and (heavy, light). The average number of draws to get dissimilar molecules will be the inverse of this, 1/[2 fF (fF – 1)], which I take to be, upon multiplication by a factor of 2, the work required: Work = 1/[ fF (fF - 1)]. The rationale for the factor of two is that two actions are required in each pair-drawing. I ignore the presumably very slight change in concentrations caused by the selection of the first molecule of a pair.

After the first-round draws have successfully resulted in a swap (the work done on the P side is accounted for below), the demon moves on to the second-round draws for the W side. However, the number of lighter-isotope molecules in W will have been reduced to fF W – 1, while the number of heavies will have increased to (1 – fF)W + 1. The abundance of lights will consequently now be fnew = (fF W – 1) /W = fF – 1/W. The change in concentration between rounds is Δf = –1/W, an expression that will be used shortly. For the second-round draws, the probability of selecting dissimilar molecules will be 2 fnew (fnew – 1), with corresponding work 1/[ fnew (fnew – 1)].

I call the work involved here "Demon Work Units" (DWUs) in analogy to SWUs. Continuing this procedure gives the total work on the W side as where the index i runs over rounds of draws; fi = fF – (i – 1)/W. To circumvent having to sum over the astronomical number of rounds required to process kilograms of material, it is convenient to turn Eq. (4) into an integral. We can do this as follows. Write the factor of “1” in the numerator of Eq. (4) as – W Δ f from the argument above regarding the change in concentration. This givesFor the P side the work emerges similarly, with W replaced by P and limits (fF, fP). The total work is thenThese integrals are standard. The lower limits give identical results but for the prefactors of W and P, which can be combined as W + P = F. The result is now a rigorous analysis of separative work shows that the correct expression is where V(x) denotes to so-called “ value function”,Equations (7) - (9) share some similarities, but differ due to the hypothetical procedure imagined here; real enrichment process do not get to pick and choose what molecules they operate on. Perhaps somewhat surprisingly, however, they give remarkably similar numerical results. Figure 3 shows DWU vs. SWU for 13 combinations of (fF, fP), with both evaluated for P = 1 and fw = 0.0025. The correlation is remarkably tight: y = 0.9517x – 1.589 (r 2 = 0.9987). The demon model underestimates SWU by a few percent (for example, 205 vs. 219 at the topmost point), but this can be regarded as acceptable given the pedagogical intent. Similarly good correlation holds for other reasonable tails concentrations.The counterintuitive behavior of separative work alluded to in the Introduction originates with the logarithmic dependences in Eqs. (7) and (9); small changes in the argument of a logarithmic function, particularly if a denominator is involved, can have significant consequences. This behavior is exemplified in Fig. 4, which shows the DWU cost and product resulting from processing F = 1000 units of feed material to a given final concentration, assuming a feed concentration of f_F = 0.0072 and a tails concentration of fw = 0.0025. To get to reactor-grade product of f_P = 0.04 requires 710 units of work and yields only 125 units of product. Processing this product up to a bomb-grade level of f_P = 0.90 requires less than half as much additional work, 309 units, but yields a paltry 5.24 units of product. If his product is kilograms of hex, it will contain only about 3.2 kg of ²³⁵U; the bare critical mass of this isotope is about 45 kg. The ratio of product to work diminishes steadily with increasing f_P.

As another way of looking at how less work is required to go from a somewhat enriched intermediate product to a highly-enriched final product than is required to get to the intermediate product to begin with, we can compute the number of particle exchanges (not draws) the demon has to execute. Suppose that we start with F = 100,000 molecules with f_F = 0.0072, from which we wish to ultimately isolate product with f_P = 0.90 by proceeding in two steps: First isolating product enriched to f_P = 0.2, and then enriching that product to f_P = 0.9. Both steps are assumed to have tails fw = 0.0025. For the first step, Eq. (3) indicates that, rounding off to the nearest whole number, P = 2380 molecules. Initially, only 0.0072(2380) = 17 of these will be of the desired light isotope. But we want to enrich this to f_P = 0.2, which demands having 0.2(2380) = 476 light-isotope molecules on the P side of the chamber. Hence, the demon will have to shift 459 molecules from W to P in this step. He then executes the second step, beginning with F = 2380 and f_F = 0.2. Here Eq. (3) indicates that this will require P = 524. He subdivides the new feed chamber accordingly, isolating 0.2(524) = 105 light molecules on the P side. But what is desired is 0.9(524) = 472, which will require shifting 367, or only about 80% as many actions as were required in the first step. Working through the numbers in this way can be helpful, but the ultimate metric is the work involved according as the number of drawings.

5. THE WORLD SWU SITUATION
According to the World Nuclear Association, worldwide enrichment capacity as of 2020 was about 66.7 million kg-SWU per year. [4] The European enrichment corporation Urenco makes available a menu of handy online calculators to help you estimate the optimum mix of feed and waste concentrations as a function of current kg-SWU cost.[5] According to the United States Energy Information Administration, the average per kg-SWU cost of enrichment services for civilian owner/ operator power reactors in 2021 was about $100.[6] Only a small fraction of this cost is that of the power required to run the centrifuges: one site estimates that a modern centrifuge consumes only about 50 kilowatt-hours per kg-SWU of separative work.[7] The power consumption to run a centrifuge is very modest, only about 35 Watts.[8] In short, the world has plenty of enrichment capacity.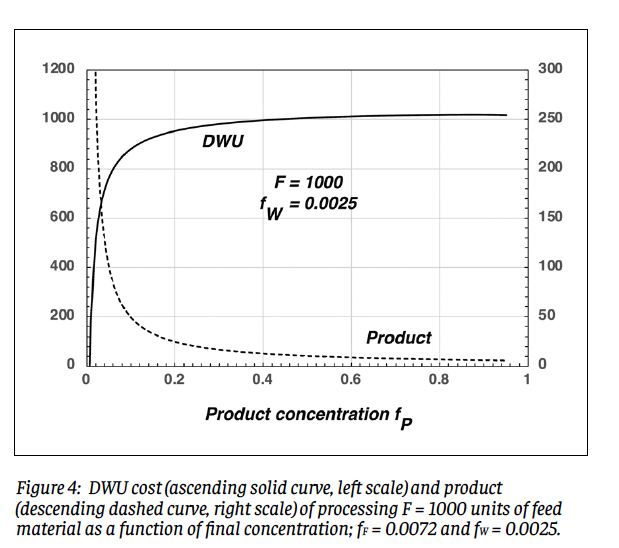

Separative work is a quantity that is conceptually straightforward, challenging to analyze rigorously, and then easy to compute once the relevant formula has been established. It is hoped that this article will help interested but non-specialist readers develop a deeper appreciation of this important issue. However current nuclear affairs resolve themselves, enrichment and its relation to potential proliferation will remain concerns for the foreseeable future.

REFERENCES
[1] K. Cohen, The Theory of Isotope Separation as Applied to the Large- Scale Production of ²³⁵U. (New York, McGraw-Hill, 1951). Available at https://www.scribd.com/doc/40224259/Karl-Cohen-The-Theory- About-Isotope-Separation
[2] S. Whitley, “Review of the gas centrifuge until 1962. Part I: Principles of separation physics,” Rev. Mod. Phys. 56(1) 41-66 (1984).
[3] J. Bernstein, SWU for You and Me. https://arxiv.org/abs/0906.2505 (2009).
[4] https://world-nuclear.org/information-library/nuclear-fuel-cycle/ conversion-enrichment-and-fabrication/uranium-enrichment.aspx
[5] https://www.urenco.com/swu-calculator
[6] https://www.eia.gov/uranium/marketing/
[7] https://www.sizes.com/units/separative work unit.htm
[8] R. L. Garwin, HEU Done It, http://fas.org/rlg/030005HDI.pdf

Top